Introduction to Fourier analysis of time series

How to detect seasonality, forecast and fill gaps in time series using Fast Fourier Transform

Mehmet E. Yavuz (2021). Fourier Series Animation using Harmonic Circles (link), MATLAB Central File Exchange. Retrieved January 24, 2021.

In this article, I will show you the uses of the Fourier transform in time series analysis. We will use the Fast Fourier Transform algorithm, which is available in most statistical packages and libraries. Visualisations and code examples in Python supplements this article.

All are available in this notebook (Google Colab).

Although this topic often seems complicated, I will convince you that even basic use of Fourier analysis can give good results.

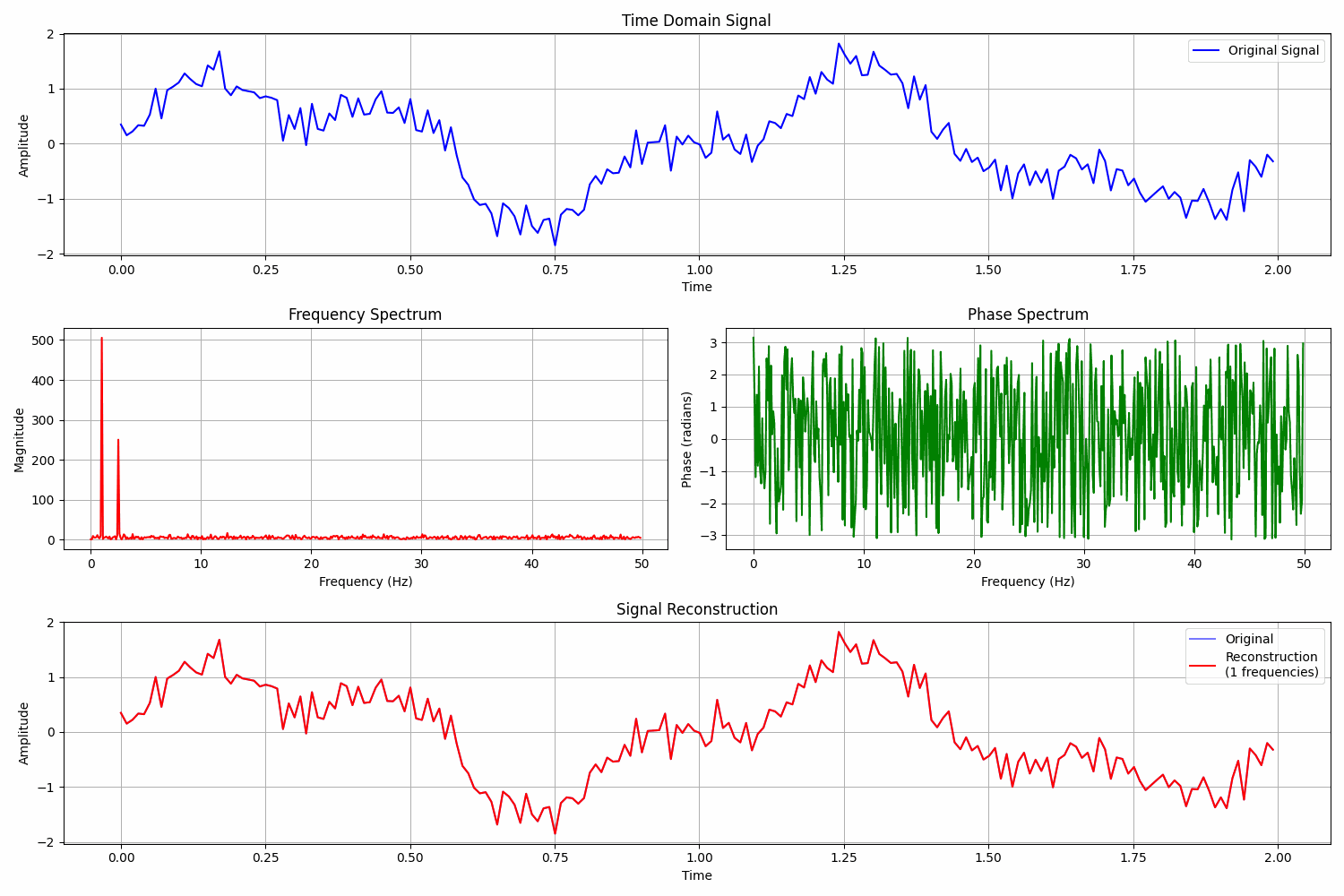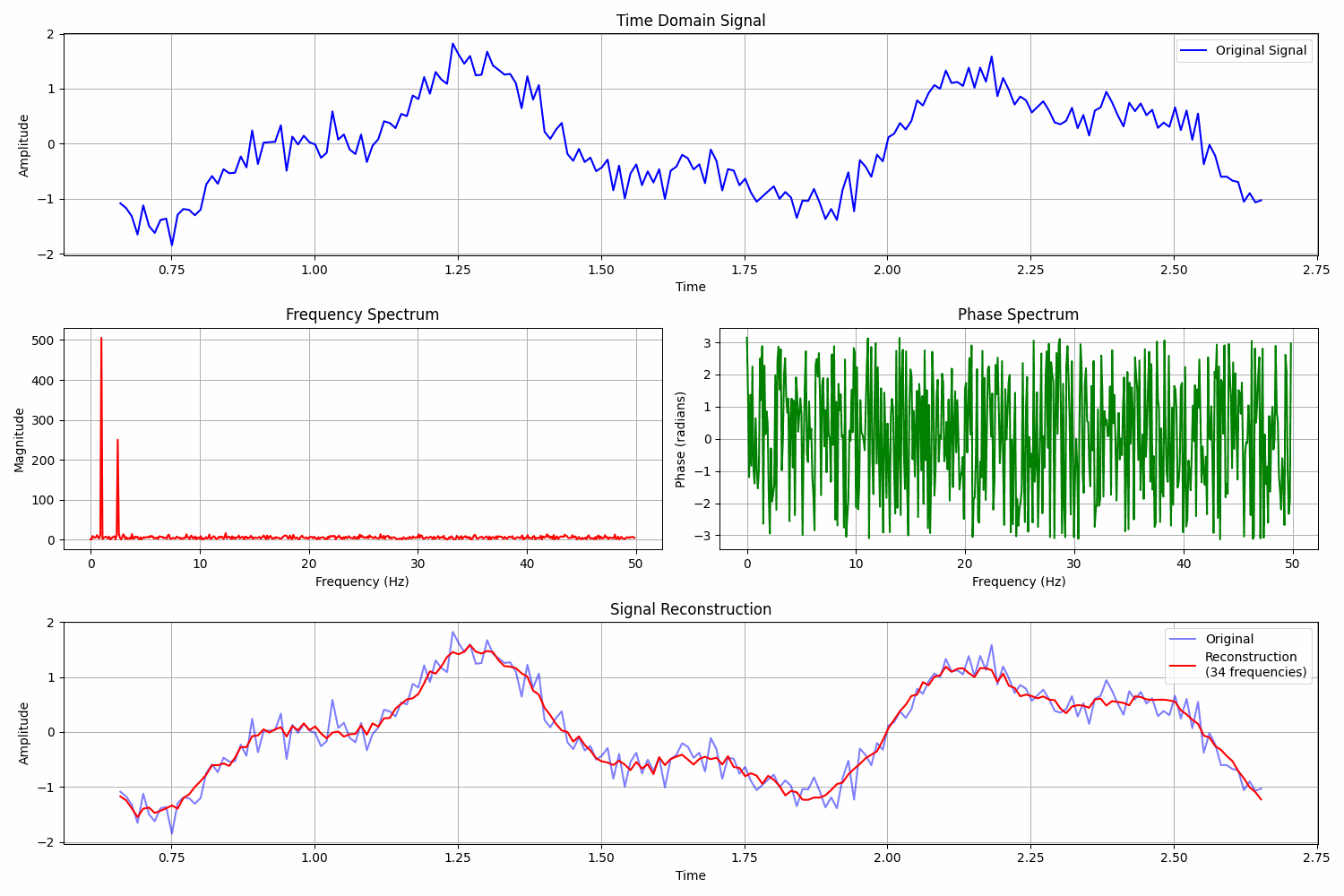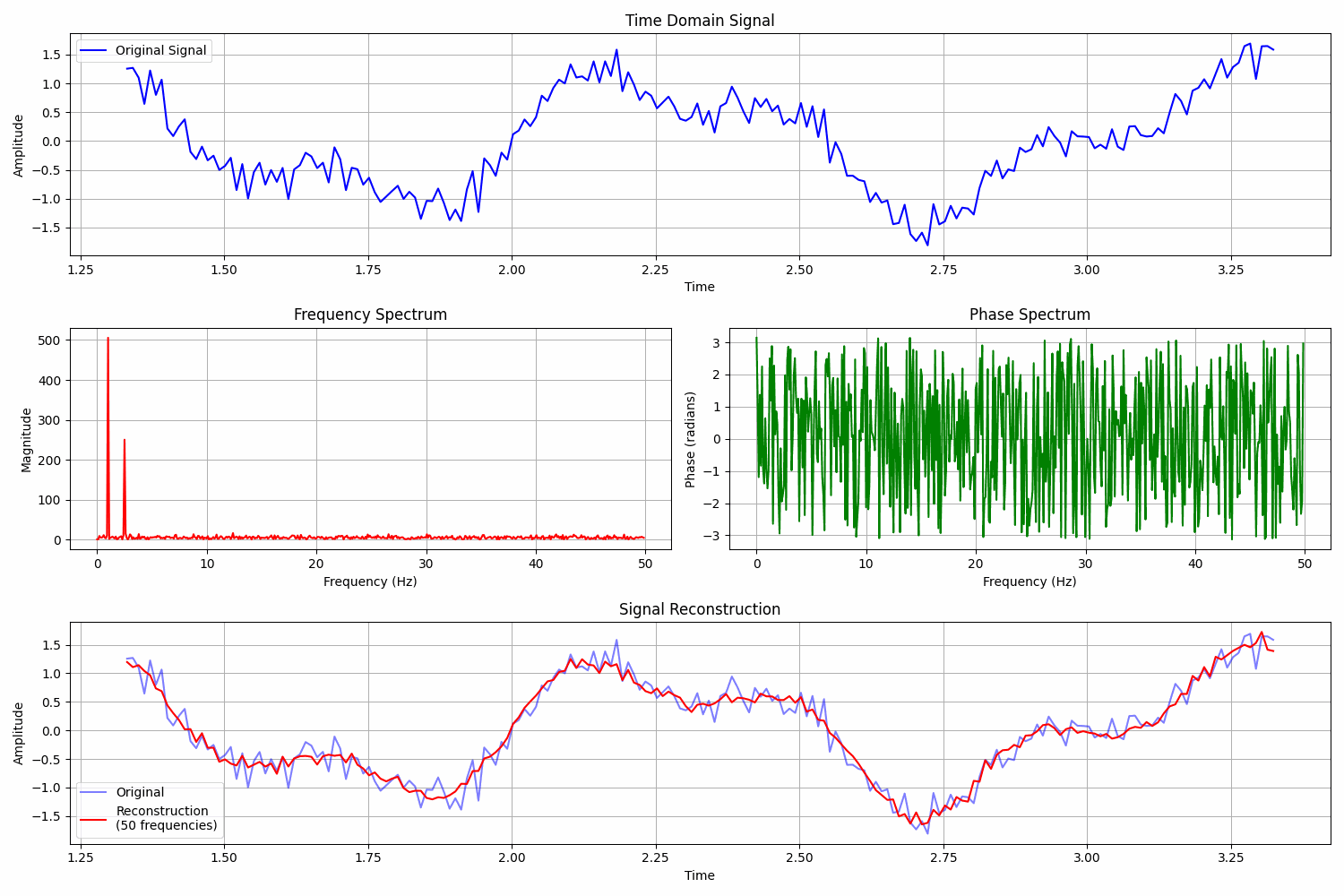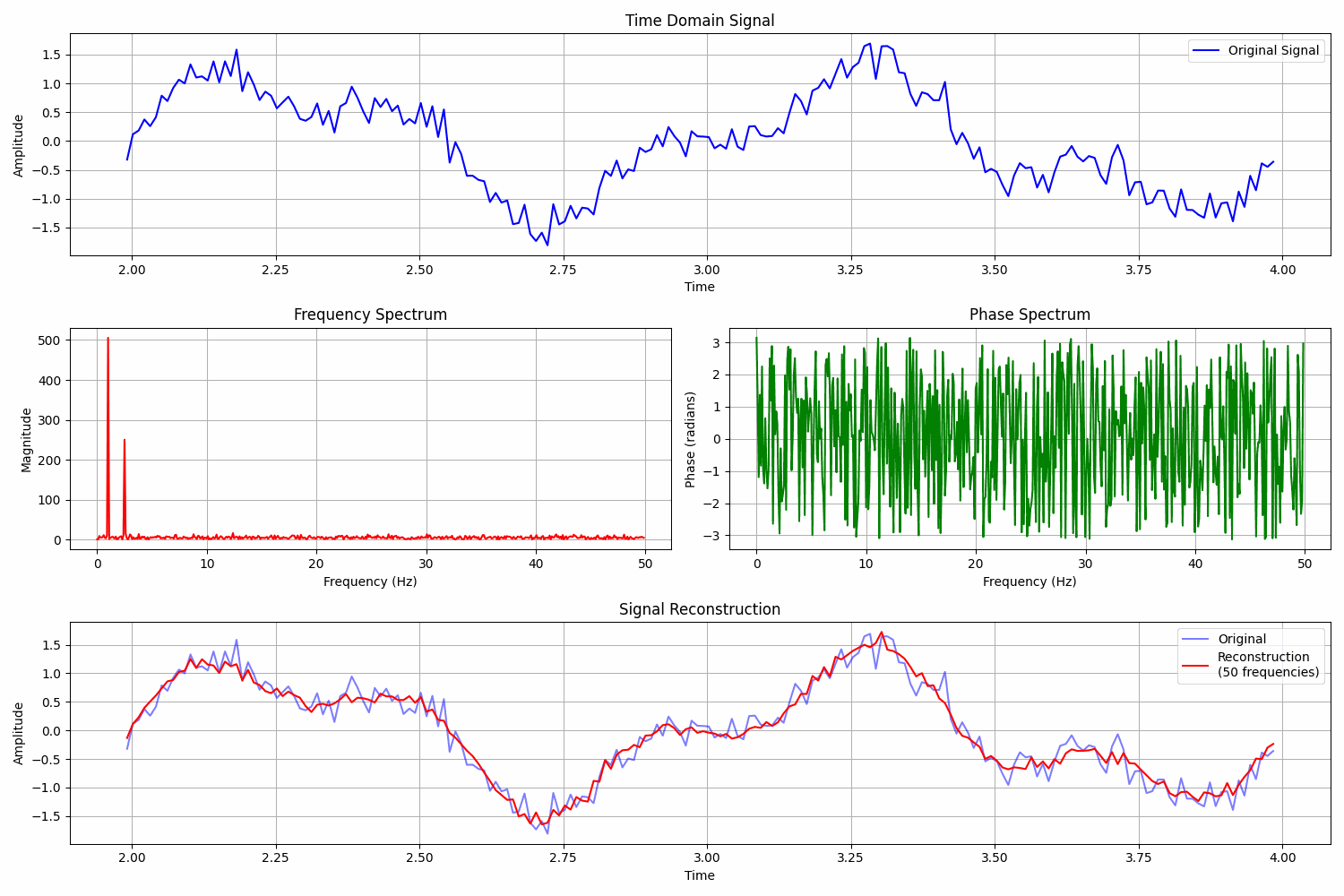
How to analyse weather data using Fourier analysis

Let’s assume that we work on some weather data.

In our dataset is the average daily temperature for a certain location.

Although there are outlier measurements in the dataset, the general trend is consistent over time. (fig. by author)

As we can see, a sinusoidal trend prevails throughout the year at a certain fixed frequency. If we can know what frequency this is, we can decompose the seasonality of this time series. This could be useful for improving forecasts or dealing with missing measurements.

Fourier analysis

Our goal is to take this single-variable periodic time series and decompose it into simpler periodic functions.

According to the theorem formulated by Joseph Fourier, any periodic function, no matter how trivial or complex, can be expressed as a composition (combination) of periodic components, known as the Fourier series.